Activity:
Split students into small groups.
Provide 3 identical sheets of paper to each group.
Give each student group a number from 2–8.
Instruct student groups to fold each piece of paper according to their assigned number using the the following instructions.
Folding the Papers:
Sheet 1: Accordion fold one less time than the number the group was assigned, n – 1.
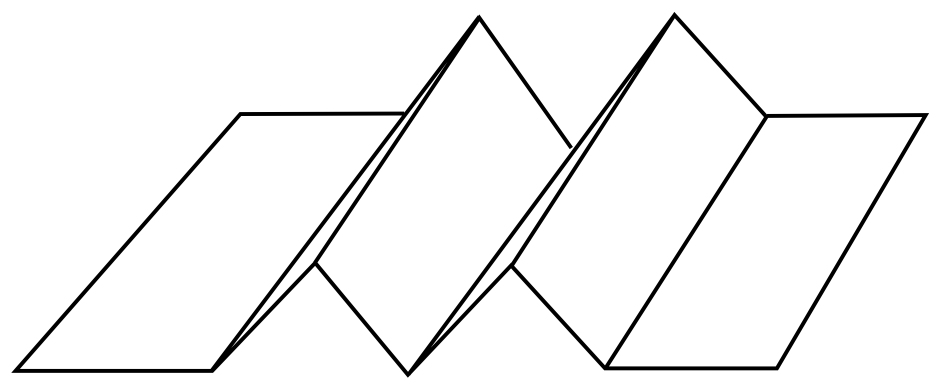 (ref)
(ref)Sheet 2: Accordion fold one less time than the number the group was assigned, n – 1. Then, again, accordion fold the result one less time than the number the group was assigned, n – 1.
Sheet 3: Repeatedly fold in half n times.
 (ref)
(ref)Unfold and count the resulting rectangles created by the folds. Record the results in a table like the one below.
No folds independent of input: O(1), constant time
Sheet 1: Folding linearly with input: O(n)
Sheet 2: Folding polynomially with input: O(n²)
Sheet 3: Folding exponentially with input: O(2ⁿ)
| n | n² | 2ⁿ |
| 1 | 1 | 2 |
| 2 | 4 | 4 |
| 3 | 9 | 8 |
| 4 | 16 | 16 |
| 5 | 25 | 32 |
| 6 | 36 | 64 |
| 7 | 49 | 128 |
Discuss the results.
Why do the folding instructions correspond to the complexities in the table?
If the paper folding continued to larger numbers of n, how would the results scale?
Compare the different thicknesses of the resulting folded sheets.
- A common claim is that Sheet 3 cannot be folded more than 7 times. Why?